![]()
As was stated in the fractal generation examples, this particular Lindenmayer fractal (shown above) is not so visually appealing but is mathematically interesting. This time, let's predict what type of value we will get for the capacity dimension of Cantor's dust. We have already noted that this fractal is produced by removing the middle third of every line at each iteration, and thus the limit of its length is zero (even though the limit of the number of lines is infinite). (A short proof of the zero length is found at the bottom of this page.) A length of zero suggests a dimension less than 1, which would be an incredibly strange result. We also intuitively expect that any object that exists should have a dimension greater than 0, and certainly not negative (hopefully), so we predict a value between 0 and 1 exclusive.
Here we use the same technique as with the Koch snowflake. Since the middle third of every line is removed on each iteration, thus each line is replaced by two identical copies of itself, each with one third the length of the original. And when determining the dimension of the snowflake, we decided that the dimension of each line segment that makes up a fractal is the same as the dimension of the fractal itself. So for the capacity dimension of Cantor's dust, we can use P = 2 and S = 3:
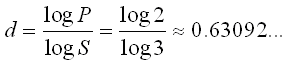
Just as expected, our result is between 0 and 1, somewhere between the dimension of a point and the dimension of a line.
Georg Cantor invented this fractal to describe a set of numbers that he had defined, which is now called Cantor's set. It involves the unit interval in the ternary number system. The unit interval is the set of reals between 0 and 1. The ternary number system is the system with 3 digits (as opposed to 2 for binary and 10 for decimal). Cantor's set consists of all real numbers on the unit interval which do not contain a 1 in ternary form.
How does the Cantor's dust fractal relate? Conceptualize the first iteration (a single line) as the unit interval. The second interval removes the middle third of this line. Now on the left, we have a line that represents the reals in the unit interval whose first ternary digit is 0. The middle line that was removed represented those numbers whose first ternary digit is 1, and on the right we have the line representing numbers with first ternary digit 2. Upon the next iteration, we remove the middle third of both lines. Thus, from the numbers starting with 0, we remove those with 1 for their second digit, and the same for numbers starting with 2. The next iteration removes numbers with third digit 1, and so on. This process is illustrated below. As the number of iterations approaches infinity, the resulting fractal limit represents exactly Cantor's set.
First iteration |
|
Second iteration |
There is another interesting property to be noted about the Cantor's set: it is uncountable. This is a special type of infinite size. Cantor showed that the set of all rational numbers is "countably infinite" and the set of all reals is "uncountably infinite", thus proving that the set of reals is larger than the set of rational numbers. Here we briefly show that Cantor's set is also uncountable. We denote Cantor's set by C. Now, take the binary expansion of the unit interval and call it B. This set is a closed consecutive sequence of real numbers, and thus is uncountable. To show that C is uncountable, we show that it is the same size as B. To do this, we define a bijection between B and C. We know that all members of B have digits 0 or 1 because they are binary, and all members of C have digits 0 or 2 by definition. We can map a member of C into B simply by replacing all digits that are 2 by 1. Conversely, mapping a member of B into C is performed by replacing all 1's with 2's. Thus every member of C maps to a unique member of B and vice versa. We have defined a bijection between C and B, thus the sets are the same size, and so since B is uncountable, C is as well. QED
At each iteration, one third of every line segment is removed, so if the length of the first iteration (n = 0) is 1, then the length at iteration n is (2/3)^n. We take the limit:
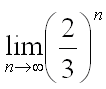
Since (2/3) < 1, the length decreases as n increases, and thus the length of the Cantor's dust fractal is 0. QED