Robert Hunter
Math 308, Euclidean Geometry
Term Project, Fall 2003
The Shoemaker's Knife Problem - An Application of Inversion
Pappus of Alexandria (who
wrote in the time of Diocletian, 284-305 AD) records in his Collection[i],
the following proposition:
Let two semicircles be drawn, a larger one B and a smaller one A fitted inside the first, with centres b and a, respectively, lying on a common baseline (fig. 1).
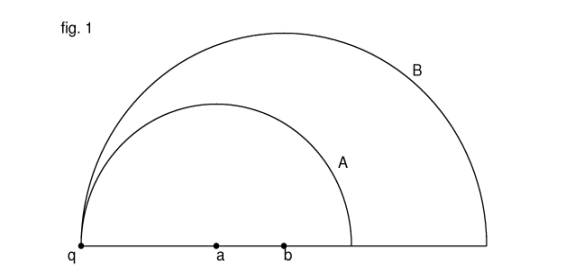
This figure Pappus calls an
άρβηλος, or shoemakers knife. Now let the
area between the two semicircles be filled with circles C0, C1, C2,... tangent to A and B
and to each previous circle in the sequence (fig. 2).
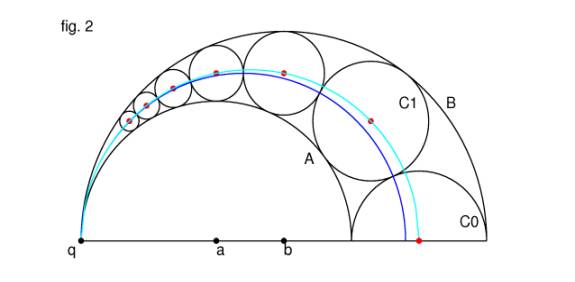
Then the following results hold for this figure:
(1)
The centres of circles C0, C1, C2,... all lie on an ellipse
(cyan) passing through q.
(2)
The points of contact of same circles all lie on a
circle (blue) passing through q.
(3)
Letting the radius of Cn be rn, the height of its centre
above the baseline is 2nrn.
That the centres of C0, C1, C2,... all lie on an ellipse
passing through q is apparent from the diagram below (fig. 3). The foci of the
ellipse are points a and b, and the sum of the distances from the foci to any
point on the ellipse is, if we allow a and b to be the radii of circles A and B
as well as their centres, a + b. It can also be shown that the lengths of the
major and minor axes of the ellipse are a + b and 2√―a――b
, respectively.
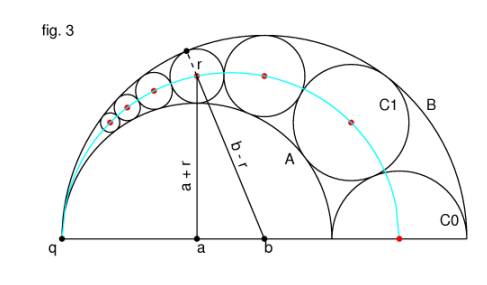
In order to prove the remaining two statements of the
proposition, we shall make use of an insightful trick. Before we can do this,
though, we need to make a diversion of some length.
Inversion
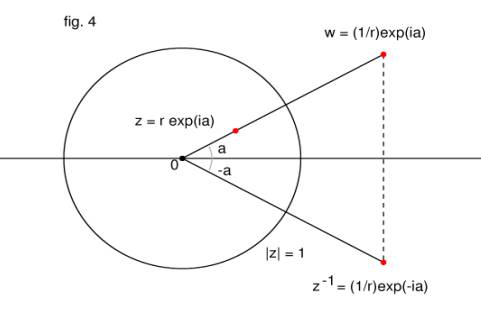
In the complex plane, the algebraic inverse z-1 of a point z = reiθ is the point that
results from taking the reciprocal length and then reflecting across the real
axis, viz. (1/r)e-iθ. If we just take
the reciprocal length but not the reflection, we get the geometric inverse
of z, or w = (1/r)eiθ, = 1/z―. w is the inversion of z in the unit
circle, |z| = 1 (fig. 4).
We can generalize this to inversion in a circle K of radius R
centred at point q by:
(1) translating by q
(centres K at the origin)
(2) scaling by 1/R
(shrinks K to the unit circle)
(3) inverting in the
unit circle
(4) scaling by R (K
returns to its original size)
(5) translating by q (K
returns to its original position).
The resulting formula is w = R2/( z― - q―
) + q. To check that this formula performs as required, note that if z q = reiθ, w - q = (R2/re-iθ) = (R2/r)eiθ, which is in the
same direction as z q from the centre of K and has the reciprocal length with
respect to the scaling factor of R:
(r/R)* ((R2/r)/R) = 1
Also note that |z q| * |w q| = R2.
We shall now examine the effect of inversion on circles and
lines. Let K, the circle in which we are inverting, have radius R and be
centred at q as before, and, for simplicity, assume q = 0.
(1)
Since any point on a line through the origin, with the exception
of 0 itself, is mapped by the inversion to another point on the line, and any
point on the line, other than 0, is the image of some other point on the line,
the image of the line under inversion is, if we ignore this one exception, the
same line. In order to patch up the hole at 0, we make the convention that the
point at infinity (∞) is mapped to 0,
and vice versa. Thus inversion in a circle is 1-1 and onto the extended complex
plane. (We denote this function by IK.)
(2)
Lines not through the origin are mapped to circles passing through
the origin (understanding that the line contains the point at infinity, which
is mapped to 0), and vice versa[ii]
(fig. 5).
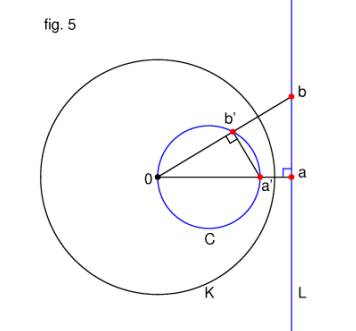In this figure,
point a, lying on the intersection of L and the perpendicular through 0, is
mapped to a point a on the perpendicular. Point b, which is mapped to the
point b, is any other finite point on L. C is defined to be the circle with
diameter 0a. We determine that IK(L)
= C as follows.
From the formula |z q| * |w q| = R2, above, we obtain
|a|*|a| = R2 and |b|*|b| = R2, which implies
|a|/|b| = |b|/|a|. Since angles a0b and b0a are the same angle, this implies that the two
triangles Δa0b and Δb0a are similar. 0ba,
corresponding to 0ab, must therefore
be a right angle, i.e. the line segment 0a subtends a right angle to b. b
thus lies on C.
Since b was taken to be an arbitrary point on
L (other than a and ∞, whose images, a
and 0, clearly lie on the circle) the image of every point on L must lie on
this circle.
Analogously, the image of every point on C
must lie on L. Thus, the image of L under the inversion must be all of C.
(3)
Circles not passing through the origin are mapped to circles not
through the origin (fig. 6).
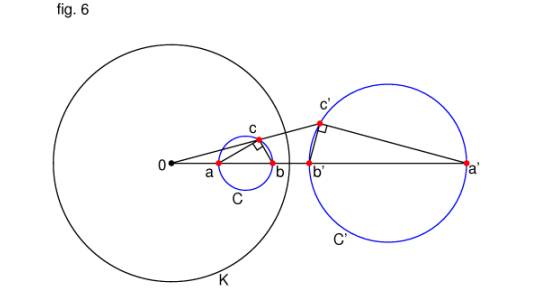
In this figure, points a and b, lying on the ray from 0 through
the centre of C, are mapped to the points a and b, respectively. Point c,
which is mapped to c, is any other point on C. C is defined to be that circle
with diameter ba. We determine that IK(C)
= C as follows.
As in case
(2), above, triangles
Δa0c and Δc0a are similar,
as are triangles Δb0c and Δc0b.[iii]
Thus 0cb = 0bc and 0ca = 0ac, since these are corresponding angles in
similar triangles. bca = 0bc - 0ac, = 0cb -
0ca, = acb. Since C is a circle and ab its diameter, acb is a right
angle. Thus bca is also a right angle, i.e. the line segment ba subtends
a right angle to c. c thus lies on C.
Since c was taken to be an arbitrary point on
C (other than a and b, whose images, a and b, clearly lie on C) the image of
every point on C must lie on C.
Analogously, the image of every point on C
must lie on C. Thus, the image of C under the inversion must be all of C.
(4)
Circles orthogonal to the inverting circle K are mapped onto
themselves (fig. 7). That this is the case follows from the fact that the
images under IK of figures tangent
at a point P are again tangent, at the point IK(P).[iv]
Circle C is tangent to the lines 0b and 0c at points b and c, respectively.
Thus the image of circle C, call it C, is also tangent to the lines 0b and 0c
(the lines 0b and 0c being mapped onto themselves) at points b and c (these
being unmoved by the inversion). The only circle that meets these conditions is
C itself, so C must be C.
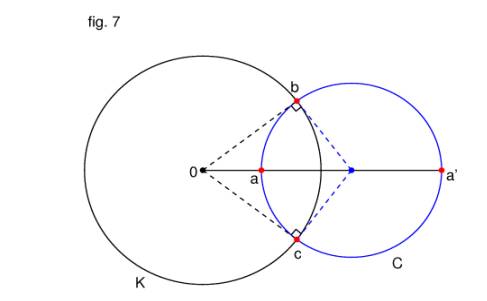
Note that, although IK(C) = C, i.e. the points of C are all mapped
onto C, the centre of C is not mapped to itself, since the centre of C lies
outside of K and its image under the inversion on the inside.[v]
Back
to the Shoemaker's Knife Problem
We are now equipped to
prove the remaining two parts of the original proposition:
(4)
The points of contact of circles C0, C1, C2,... all lie on a circle
passing through q.
(5)
Letting the radius of Cn be rn, the height of its centre
above the baseline is 2nrn.
If we consider how to draw the figure
(referring to fig. 2), it appears to be the result of taking a vertical column
of circles, sandwiched between vertical lines on each side, and then somehow
squeezing all this over to a point on the baseline. The bottom circle in the
column would remain fixed, the two vertical lines would be bent into the
circles A and B, and the remaining circles would be squeezed in to fit between
A and B.
This suggests an inversion about a circle
orthogonal to C0 and
centred at the point at which circles A and B meet (fig. 8).
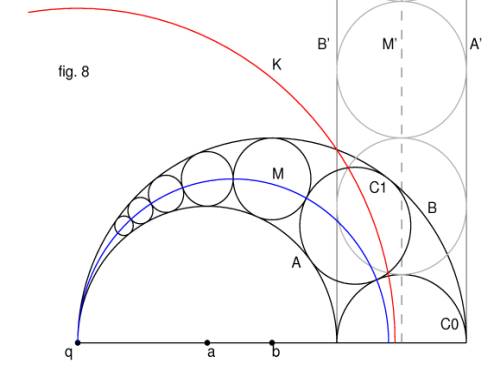
Here K is the circle centred at q which meets C0 at
right angles. Thus IK(C0) is the same circle. The
images of the vertical lines A, B, and M under inversion in K are all
circles, A, B, and M, respectively, passing through q and symmetric about the
baseline (the perpendicular through the centre of K). Circles C0, C1,
C2,... we know are inverted to another string of circles C0,
C1, C2,.... Since each point of intersection is mapped to
a single point in the image, these must still be in contact with each other and
be tangent to the circles A and B. Thus inversion in K produces the desired
figure.[vi]
The points of contact of the stack of circles C0, C1,
C2,... all lie on the vertical line M, thus after inversion they
must all lie on M, the image of M under IK. This proves the second part of the
proposition.
In order to prove the third statement, simply
choose any circle Cn and invert the figure about that circle Kn, centred at q,
which is orthogonal to Cn (fig. 9).
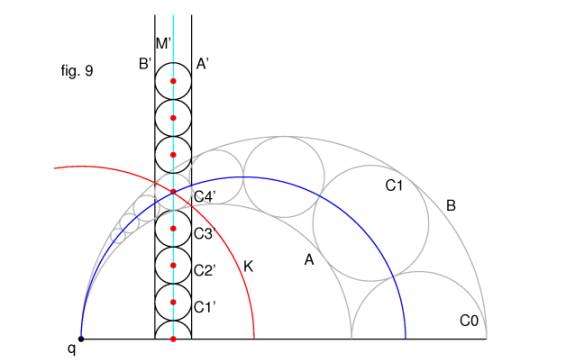
The circle Cn is then unmoved,
with C0, C1,..., Cn-1, Cn+1, Cn+2... stacked above
and below it. Circles A and B are transformed into vertical lines, as before,
although now they sandwich this new column. Since the image circles all have
the same radius, rn, as Cn, one can
immediately see that the centre of Cn lies a distance 2nrn above the
baseline. This proves the final statement of the propositon.
References
[1]
Needham, Visual Complex Analysis, Clarendon Press, Oxford, 1997.
[2]
Heath, A History of Greek Mathematics, Volume II, Dover, 1981.
[3]
Churchill and Brown, Complex Variables and Applications, McGraw-Hill,
1984.
The
historical background is to be found in Heath. The proof using inversion, as
well as most of the theory on inversion, I took from Needhams book. The
drawings are all original and were produced by PostScript programming.
Acknowledgement
I
would like to thank Professor Casselman for suggesting this topic, as well as
for providing two of the three references.
Endnotes