Archimedes: On Conoids and Spheroids

Propositions 19 - 22

Jacqueline Sheppet

Math 308 with Bill Casselman

Archimedes of Syracuse [287 – 212 BC] was the greatest mathematician of his time, and is still considered one of the greatest mathematicians of all time. His work was both prolific and painstakingly detailed often ending with the reductio-ad-absurdum proof technique. His ‘method of exhaustion’ [calculating an area by approximating it by the areas of polygons] technique was used quite extensively throughout his work and is considered a forerunner to modern methods of integration.

Some of the most famous work by Archimdedes include: Measurement of a Circle, Quadrature of a Parabola, On the Sphere and Cylinder, On Spirals, On Conoids and Spheroids, and his volume describing his technique called The Method.

In On Conoids and Spheriods, Propositions 19 – 22, Archimedes proved geometrically that the volume of a conoid [now known as a paraboloid] is exactly half of that of the cylinder that tightly encloses it. This is a reproduction of his proof, using his method of exhaustion.

Consider a 2 dimensional parabola rotated around its axis of symmetry. Consider the cylinder that would enclose this shape. The volume of the cylinder is exactly twice the volume of the paraboloid.

The general equation of the parabola is y proportional to x² although, my drawings show the paraboloid inverted, this does not affect the results.

A cross section of this 3 dimensional solid looks like this:

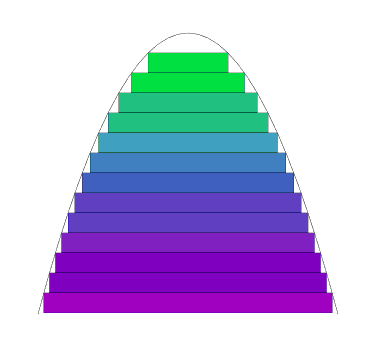
We can approximate the volume of the paraboloid with cylindrical disks. There are two ways to do this: by inscribing cylinders

It should be clear that the top most circumscribed slice is equal to the top most inscribed slice. I have coloured them to indicate that their volumes are equal. For example, that top green slice is clearly the same size despite the paraboloid being segmented differently. We subtract all the equal volumes until we are left with the nth cylinder from the circumscribed cylinder alone. This technique was favoured by Archimedes, and is an example of his method of exhaustion.

I_n is the inscribed solid

C_n is the circumscribed solid

I_n is the cylindrical solid

These solids are therefore made up of the separate pieces.

let I_n = i₁ + i₂ + i₃ + ... + i_n

C_n = c₁ + c₂ + c₃ + ... + c_n

S_n = s₁ + s₂ + s₃ + ... + s_n

i₁ = 0

c₁ = i₂, c₂ = i_3, c₃ = i₄ and so on....

In general c_r-1 = i_r

Here it gets interesting. We are left with c_n. If we make n very, very large, in other words, inscribe and circumscribe many, many cylinders on the paraboloid, that means this quantity can be made to be as small as we like.

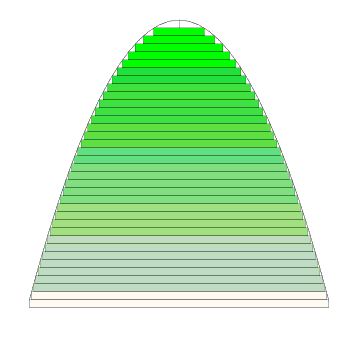
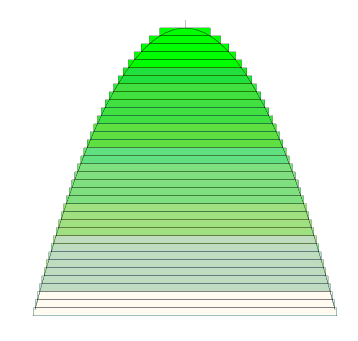
I illustrate this by reconstructing the above pictures with approximately double the number of disks.

Firstly I show close ups of the circumscribed picture from above, where n is approximately 15. (I have picked arbitrary values of n for illustration). Next to it is the picture of the circumscribed disks where n is around 35, over double the previous value of n. The paraboloid is identical in both pictures:

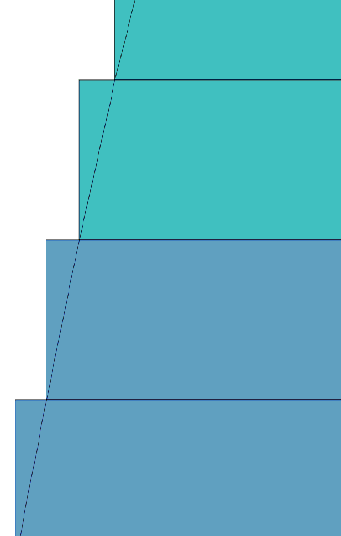
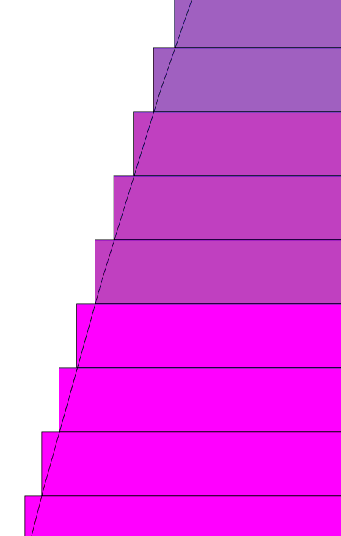
It is very clear that with the smaller disks, there is less 'error'[including too much volume for the paraboloid] from the disks being circumscribed over the paraboloid. Some of the coloured volume is simply not included anymore. As n gets very large, the 'error' goes to zero.

Secondly I show close ups of the inscribed picture from above, where n is approximately 15. (Again, these are arbitrary values of n for illustration). Next to it is the picture of the inscribed disks where n is around 35, over double the previous value of n. The paraboloid is identical in both pictures:

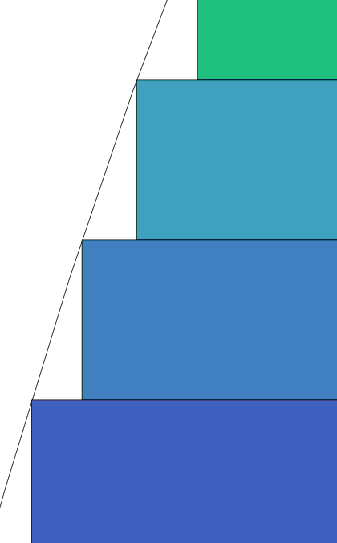
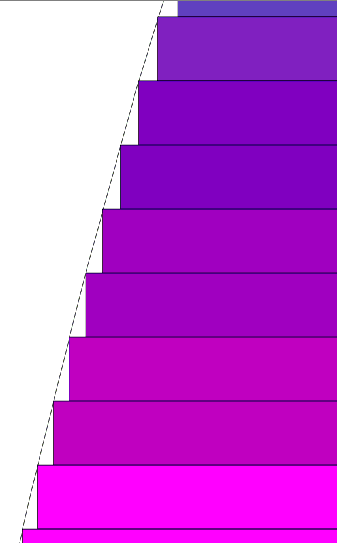
It is very clear that with the smaller disks, there is less 'error' [not including enough volume from the paraboloid] from the disks being inscribed inside the paraboloid. Some of the blank volume is now taken up by disks. As n gets very large, the 'error' goes to zero.

To see both circumscribed paraboloids in the one picture, have a look at this postscript file. You can clearly see the outline of the volumes that are no longer included. The inscribed analogue is here.

Since the disk is cylindrical, it should have the volume equal to (pi)R²h where R is the radius at that part of the paraboloid.

So for example, the cylinder that is at h height has radius of x_h, at height 2h, the radius is x₂ ... so on to height nh with radius x_n. This matches with our general parabola equation given earlier, x_n² proportional to rh, when we consider the equation of the volume of the disks. Also the r^th inscribed piece is proportional to (r - 1)h and the r^th circumscribed piece is proportional to rh. Finally, the r^th piece of the cylinder is proportional to nh [since all r pieces are uniform].

This means that we can set up the ratios of the size of the paraboloid pieces to the cylindrical pieces. In particular, for the inscribed cylinders:

If we sum up all the pieces we get:

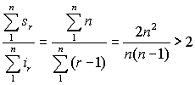
This means, when the cylinder enclosing the paraboloid is divided by the all of the inscribed pieces , its volume is more than twice that of the volume of the inscribed pieces. One of the things that simplifies this summation is the formula that sums 1 + 2 + ... + n = ½n(n + 1).

We do the same thing, but instead this time with the circumscribed disks:

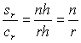
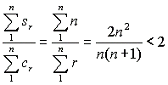
Again, this means, when the cylinder enclosing the paraboloid is divided by the all of the circumscribed pieces , its volume is less than twice that of the volume of the circumscribed pieces.

Putting together both bits of information leads to the following inequality:

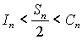
Let us think about these results. When we constructed the circumscribed disks, around the paraboloid, it seemed as if we included a bit of volume that made the total volume of the circumscribed pieces larger than that of our paraboloid. By the same token, the inscribed pieces when totalled should seem to be less than the volume of the paraboloid. So the volume of the paraboloid is somehow sandwiched between I_n and C_n.

What is S_n? The volume of this cylinder is (pi)R²h as mentioned earlier. We now consider that quantity divided by 2 and sandwiched between I_n and C_n. Imagine, that the volume of the paraboloid was < ½S_n. Then we could choose our n to be sufficiently large so that the volume of the inscribed disks were > ½S_n. Recall that I_n = i₁ + i₂ + i₃ + ... + i_n. However, this contradicts our earlier result, so clearly the volume of the paraboloid is not greater than half the volume of the cylinder.

Imagine, that the volume of the paraboloid was less than ½S_n. By the same token as before, we could also pick our n to be sufficiently large so that the volume of the circumscribed disks were < ½S_n. This too contradicts our previous result, so clearly the volume of the paraboloid is not less than half the volume of the cylinder.

This means by reductio ad absurdum the volume of the paraboloid must be exactly equal to half the volume of the cylinder. The reductio ad absurdum proof technique was favoured by Archimedes throughout all the volumes of his work. He was incredibly thorough with his proofs and showing a result using contradiction gave a very complete proof. It also seemed to work very well for many other geometric proofs, such as quadrature of the parabola, and the analogous proof to this one, areas within spirals.