Figure 1.
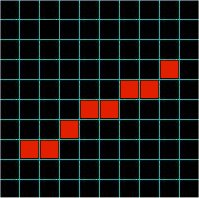
Figure 2.
| University
of British Columbia
MATH 308 Project: The Bresenham Line Drawing Algorithm December 2002. |
Ljubomir
Puhalovic
Computer Science Student No: 90329996 Professor: Bill Casselman |
Table of Content
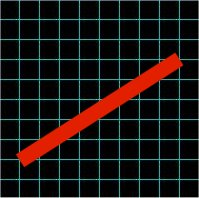
| The Bresenham Algorithm for drawing lines on the discrete plane, such as computer monitor is one of the fundamental algorithms in computer graphics. This algorithm provides the means for the fast and efficient way to represent continuous abstract lines onto discrete plane of computer display. This process is called rasterization. Assume y = mx + b represents the real variable equation of a line which is to be plotted using a grid of pixels where the two points (Ax, Ay) and (Bx, By) have integer coordinates and represent two known points on the line. The algorithm basically approximates real valued line by calculating what pixels to illuminate and to provide "illusion" of line. Since the pixels are sufficiently small, the approximation is good enough to "trick" the human eyes and to get illusion of a real line. The basic idea is shown on Figure 1 and Figure 2. Figure 1 shows the real line drawn over the pixel grid. The Figure 2 shows how is the same line approximated by "illuminating" particular pixels. |

Figure 1. |

Figure 2. |
| Given two endpoints (Ax, Ay) and (Bx, By), we can chose the start point
( x(k), y(k) ). The choice is purely arbitrary, it can be either of (Ax,Ay)
and (Bx,By) points. From this start point or pixel, we have eight possible
choices for the next pixel in the line, since each pixel is surrounded
by 8 other pixels (except border pixels). We need to isolate these eight
choices into only two choices. If we restrict the slope m for now to 0
<= m <=1 and assume Ax < Bx, we know that we can simply step in
x one pixel at a time to the right and determine what y value to choose
next. Given ( x(k), y(k) ), the next ideal pixel (the closest to the real
line) will be ( x(k)+1, y ) where y = m*(x(k)+1) + b. But we must choose
between ( x(k)+1, y(k) ) or ( x(k)+1, y(k)+1 ). These pixels represent
the one just to the right and the one to the right and one up pixel, respectively.
The following DERIVATION demo shows basic idea of Bresenham Algorithm; i.e. it shows simplified steps of "illumination" of proper pixels according to the given line. Below is complete derivation which incorporates all optimization and speed improvements of the algorithm code. To find the best "next pixel", first we must find the distances to the
two available choices from the ideal location (of the real line). Distance
between pixel-to-right and ideal pixel is: d1 = y - y(k) and the distance
between pixel-to-right-and-up and ideal pixel is: d2 = (y(k)+1) - y. So
we can simply choose subsequent pixels based on the following:
Instead of comparing the two values to each other, we can simply evaluate
d1-d2 and test the sign to determine which to choose. If d1 > d2 then d1-d2
will be strictly positive, and if d1-d2 is strictly positive, we will choose
pixel-to-right-and-up. If d1-d2 is negative or zero, we will choose pixel-to-right.
In addition to this optimization, Bresenham Algorithm suggests to optimize
more. If we evaluate d1-d2 as follows:
This last equation can be simplified by creating a new decision variable
P(k) = dX * (d1-d2). This will remove the divisions (all integer operations
for faster and efficient computing) and will still keep the same sign for
the decision because dX variable is always positive (dX = abs(Bx - Ax)
- absolute value).
Using described approach, decision variable can be computed very efficiently,
but it still requires evaluation of P(k) for each point (pixel) along a
line. Since line entity is linear in its nature, P(k) change will be linear
as well, therefore we can evaluate subsequent P(k) values incrementally
by finding a constant change in P(k) for each subsequent pixel. By evaluating
an incremental change of the decision function P = dP = P(k+1) - P(k) we
can evaluate by substitution dP as follows:
The only remaining thing is to decide what is the initial value of P(0).
This can be decided by evaluating equation P(k) = 2*dY*x(k) - 2*dX*y(k)
+ 2*dY + dX*(2*b - 1), so for zero, we get:
|
| The "First Octant" term refers to all the lines with a slope m between
0 and 1 (0 <= m <= 1).
The OCTANTS demo demonstrates octants and shows the general direction for drawing lines for each octant. The summary of the basic steps of the algorithm for "First Octant" is following:
|
| The basic idea of the Bresenham Algorithm is shown is the previous section, but the algorithm can be easily extended to all other lines, not just the lines with slope between 0 and 1. One subset of the cases is concerned with lines with slope from -1 to 1. In the previous derivation when we checked the decision variable, we always incremented x and y by positive one. The dX and dY values are always positive regardless of which line is chosen (with slope from -1 to 1). If we keep the start point as point (Ax, Ay), we can determine the sign of the values to increment. If Ax < Bx, we know that x will be incremented by one, and if Bx < Ax, we know that x will be decremented by one (or incremented by -1). The same principle is used for the y values, if Ay < By, y will be incremented by one; and if By < Ay, y will be decremented by one. In essence, this proposed solution only changes increments for x and y, decision variable is still the same. The algorithm is basically the same, in some sense we are just "moving" our domain of calculation in the "First Octant"(see OCTANTS demo). |
| The general solution of the Bresenham Algorithm must check for the slope of the line, is it within our previous bounds where x is independent variable or is it where y is independent variable. Each "type" of lines must be drawn differently. With slopes greater than 1 or less than -1, we must take the previous implementation and swap all x and y values to "move" the calculations back into the "First Octant". For the general solution, this includes swapping dX and dY values, as necessary. In general, the Bresenham Algorithm, have no floating point numbers, no divisions and it can be implemented using bit shifting as multiplying operation. This is what this algorithm makes so efficient and fast. |
Demo implementation of various line
drawings
| Demo implementation of the Bresenham Algorithm implements algorithm
for the lines in all directions. It shows a screen-like pixel grid and
a few examples of lines drawn using the Bresenham Algorithm. After the
demo is executed in a Ghostscript, user is able to manually enter any two
endpoints of the line in order to view the required line drawing. The syntax
is: "Ax Ay Bx By bres", where Ax, Ay, Bx, and By arguments all must be
integers.
Please click HERE or at the image below to retrieve the demo in PostScript format. |
In producing this project web page the following tools are used:
Journal, Volume , Number 1. http://graphics.cs.ucdavis.edu/GraphicsNotes/Bresenhams-Algorithm/Bresenhams-Algorithm.html |