The Theorem

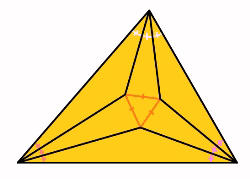
Morley's Theorem states that if you trisect the angles of any triangle then the lines meet at the vertices of an equilateral triangle.

In Morley's own words:

"If a variable cardioid touch the sides of a triangle the locus of its center, that is, the center of the circles on which the equal circles roll, is a set of 9 lines which are 3 by 3 parallel, the directions being those of the sides of an equilateral triangle. The meets of these lines correspond to double tangents; they are also the meets of certain pairs of trisectors of the angles, internal and external, of the first triangle." <ref:1>

Morley was the first to arrive at this result in 1899 based on his results on algebraic curves tangent to a given number of lines. One interesting thing about this theorem is that it is rather difficult to prove directly. Since the discovery of the theorem, more backward proofs than direct proofs have been developed. We are going to look at some of them.