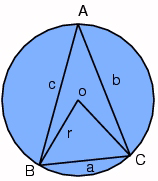
| Sine Law
a/sin(A) = b/sin(B) = c/sin(C) = 2r, if r=0.5, c=
sin C; b=sin B; a=sinA.
 Download ps file
Download ps file
 Click to enlarge
Click to enlarge  Download ps file
Download ps file
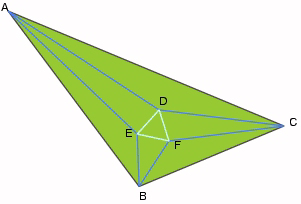
PROOF Bankoff starts
out with a large triangle ABC, with angle trisectors drawn at points
A, B and C. From the above figure we know that A+B+C = 180o.
Note that  ADC ADC
= 180- A/3 - C/3
= 180 - (A+C)/3
= 180 - (180-B)/3
= 120+ B/3
= (360 +B)/3
sin  ADC
=sin((360+B)/3) =sin((180-B)/3)--- (i) ADC
=sin((360+B)/3) =sin((180-B)/3)--- (i)
For simplification, let A = 3 ,
B= 3 ,
B= 3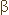 , C= 3 , C= 3 .
this implies .
this implies  + +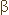 + + =60o. if we assume that the radius of the circle circumscribed
around
=60o. if we assume that the radius of the circle circumscribed
around 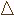 ABC
= 1 (i.e. r=1). ABC
= 1 (i.e. r=1).
using sine law we get
AB = 2sinC, AB= 2sin(3 ); );
BC= 2sinA, BC= 2sin(3 ); );
AC= 2sinB, AC= 2sin(3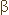 ). ).

 Download ps file
Download ps file
If we apply sine law to
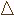 BFC, we
have BFC, we
have
BF/ sin  = BC
/ sin (180- = BC
/ sin (180- - -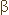 ). ).
by substitution:
BC/ sin (180- - -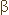 )
= 2sin(3 )
= 2sin(3 )/sin( )/sin( + +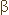 )
= 2sin(3 )
= 2sin(3 )
/ sin(60- )
/ sin(60- ). ).
Therefore BF/ sin  = 2sin(3
= 2sin(3 )/
sin(60- )/
sin(60- ), ),
i.e. BF = 2sin(3 )
sin c / sin (60- )
sin c / sin (60- ). ).
Using the identity sin(3x) = 3sin(x) - 4sin3(x),
we can simplify the identity.
sin(3x)
= 4sin(x) [ (¡Ô3/2)2-sin2(x)]
= 4sin(x) [ sin2( 60) - sin2(x)]
= 4sin(x) (sin 60 + sin(x)) (sin 60 - sin (x))
= 4sin(x) 2 sin[(60+x)/2] cos [(60-x)/2] 2sin[(60-x)/2] cos [(60+x)/2]
= 4sin(x) sin (60+x)sin(60-x).
therefore
BF= 8 sin( )
sin (60+ )
sin (60+  )sin(60- )sin(60- )sin
( )sin
( )/ sin(60- )/ sin(60- ) )
BF= 8 sin( )
sin (60+ )
sin (60+ ) sin
( ) sin
( ) ---(ii) ) ---(ii)
Applying the Sine Law,
AD/ sin( )= AC/
sin((180-B)/3) = 2r. )= AC/
sin((180-B)/3) = 2r.
Recall from above that with the assumption that the circumradius r
= 0.5, we have AC= b= sin(B). Also  =C/3.
Therefore, we have =C/3.
Therefore, we have
AD*sin((180-B)/3 = 2r sin(B) sin(C/3)
If we do similar work as in (ii), using B=3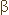 and C=3
and C=3 , we
will get , we
will get
AD = 8r sin(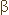 )
sin( )
sin( ) sin(60+ ) sin(60+
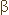 ), and ), and
AE = 8r sin( )
sin( )
sin(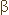 ) sin((60+ ) sin((60+ ). ).
Note that the ratio
AE/AD = sin(60+ )/sin(60+ )/sin(60+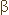 ). ).
But 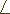 ADE
+ ADE
+ 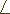 AED =
180 - A/3 AED =
180 - A/3
= (540-A)/3
= (540-(180-B-C))/3
= (360+B+C)/3
= (180+B)/3 + (180+C)/3. From here,
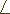 ADE = (180+B)/3
and ADE = (180+B)/3
and 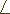 AED
= (180 + C)/3, AED
= (180 + C)/3,
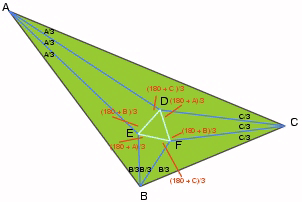
and similarly for triangles BFE and DFC.
 Click to enlarge
Click to enlarge  Download ps file
Download ps file
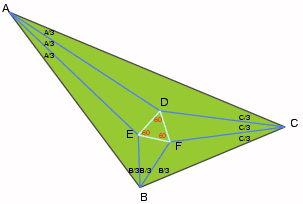
It thus follows that
the sum of angles around F, excluding DFE is 300o, or DFE
= 60o. The other two angles are similarly shown to be 60o.
 Click to enlarge
Click to enlarge  Download ps file
Download ps file
|

![]()




