![]()
The proof below is another backwards proof based
on the work of Dergiades dating from 1991.
According to Alexander Bogomolny, this proof is first
published in Greek in the bulletin of Diastasi,
a Greek Mathematical Society.<ref 2>
The original reference is from "A simple geometric
proof of Morley's Theorem", Diastasi 1991 issue
1-2 pp 37-38. Thessaloniki-Greece. <ref 2>
| The proof
uses the following lemma:
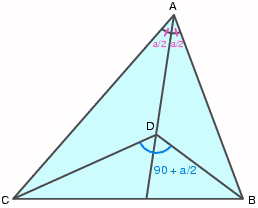
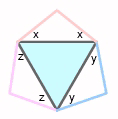
LEMMA Let PROOF Suppose that angles According to Dergiades, suppose we let Consider an equilateral triangle. Construct 3 isoceles triangles with base angles x, y, z respectively ( with the constraints x+y+z =120 and 0<x,y,z<60) on the sides on the equilateral triangle. Extend the sides of the isosceles triangles so that they intersect as shown: 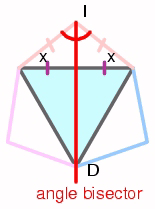
Since D is the vertex of the equilateral triangle, and I is the vertex of the isosceles triangle with base angle x, it follows that the line ID is the angle bisector. 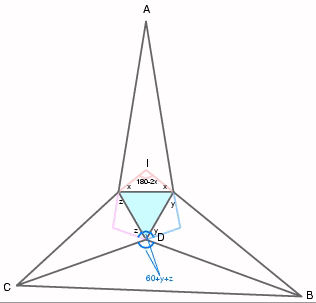
Join B and C, note that 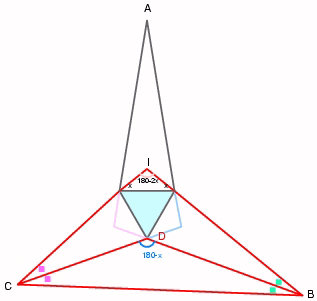
It follows that the lines drawn at points A B and C are angle trisectors. 
The last step is to prove 
we can see that by substitution, we have It follows that: |