![]()
The proof below is an indirect proof based
on the
work of Conway dating from around 1995.
![]() Click
to enlarge
Click
to enlarge ![]() Download
ps file
Download
ps file
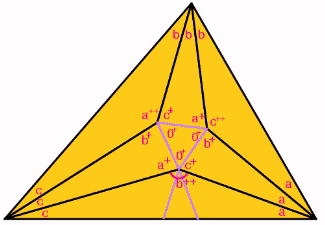
| From the above figure
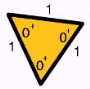
we know that 3a+3b+3c = 180o, which means that a+b+c= 60o.
Let x+ = x+60o for any angle x. since a+b+c = 60o. Let 0+=a+b+c=60o., This shows that it is possible to construct an triangle with 3 different types of angle combinations:
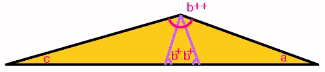
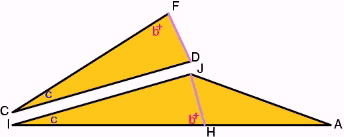
since these seven combinations of angles all have a sum of 180o. Instead of working forward, Conway worked backwards. He showed that from an equilateral triangle one can construct a triangle with any angles, i.e. with arbitrary a,b and c (that sums to 60o). According to Conway, we can make the following constructions: Type 1. Construct an equilateral triangle with length 1. Type 2. Construct a triangle with the side joining larger angles ( e.g. a+ and b+) to have length 1. for example: Type 3. Construct two lines that intersects the side opposite to b++ at angle b+, thus forming an isosceles triangle with base angle =b+. The significance of constructing the isosceles triangle
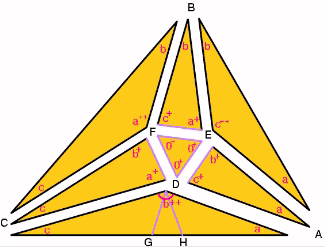
is to prove 1. 2. 3. By construction, we get JH = DF=1 The above proves that Other triangles are constructed in similar way, and we can get the following: Note that the angles at the vertex of the equilateral triangle (e.g. D) sums up to 360o. Check: (a+)+(c+)+(b++)+(0+) Since the angles at D sums up to 360o, and since the sides match due to congruency, we see that the triangles can be assembled perfectly together to form a larger triangle with angles 3a, 3b and 3c, and hence the conclusion. |