The Fifteen Puzzle
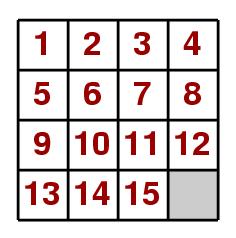 The Fifteen Puzzle has been around for over a hundred years, and has been a
craze for almost every generation. The basic form is of a 4 by 4 grid usually
made with sliding tiles in a tray. There are 15 tiles numbered 1 to 15 and the
16th place is empty as shown. Before play begins the tiles are randomly
scrambled by sliding to any starting position. The object of the game is then
to unscramble the tiles (by sliding, not lifting them) to get them into
consecutive order, with the space in the bottom right again. (This will be
referred to as the home position.)
The Fifteen Puzzle has been around for over a hundred years, and has been a
craze for almost every generation. The basic form is of a 4 by 4 grid usually
made with sliding tiles in a tray. There are 15 tiles numbered 1 to 15 and the
16th place is empty as shown. Before play begins the tiles are randomly
scrambled by sliding to any starting position. The object of the game is then
to unscramble the tiles (by sliding, not lifting them) to get them into
consecutive order, with the space in the bottom right again. (This will be
referred to as the home position.)
Sam Loyd was the man who invented the 14-15 or Boss puzzle. This was a
version where the starting position was very similar to the home position
except that the 14 and 15 were inverted. In the early 1870's he offered a $1000
reward to anyone who could solve it, which set off "fifteen fever". However
no-one claimed the prize for the simple reason that it is not solvable! The reason
shall dealt with later.
Permutations, Interchanges And Parity
It can be seen that the puzzle has 15 tiles and a space distributed over
16 squares. The number of different arrangements of tiles can be calculated:
the first square has 16 possible numbers/space to choose
from, the 2nd will have 15 possibilities...etc so there are 16 factorial possible
arrangements. This is over 20 billion different arrangements. It shall be seen
however that only 16!/2 of these are solvable.
To understand the principles involved, first look at a simpler case of
permutations (or arrangements) of a 2 by 2 grid, with 3 tiles; 1,2,3.


 These are 3 of the arrangements of the grid, with the first picture being the home
state; 9 other arrangements can be found by cycling
the 1 round to a new position and then rearranging the 2 and 3. Of course there
are 4! = 24 possible arrangements, but the other 12 can not be reached by
simple sliding moves. They would be found by performing an interchange;
ie where one tile is moved to the position of another tile or the space, which in
turn is moved somewhere else, possibly to the first tile's original position.
These are 3 of the arrangements of the grid, with the first picture being the home
state; 9 other arrangements can be found by cycling
the 1 round to a new position and then rearranging the 2 and 3. Of course there
are 4! = 24 possible arrangements, but the other 12 can not be reached by
simple sliding moves. They would be found by performing an interchange;
ie where one tile is moved to the position of another tile or the space, which in
turn is moved somewhere else, possibly to the first tile's original position.
 (ie swapping two of the tiles). One can see that the following arrangement is
not possible from the home state by following legal moves (ie sliding not
lifting):
(ie swapping two of the tiles). One can see that the following arrangement is
not possible from the home state by following legal moves (ie sliding not
lifting):
Cycles can be used to describe the permutations of objects through interchanges.
Lifting a tile up is not a legal operation, but a cycle of interchanges may
describe a set of legal sliding moves in a shorter form.
For example (3 1 2 *) would be the cycle from
 to
to
 , where * is the empty space. Of course one can see that this is the same as
(2 * 3 1) .
In a similar way, (2 * 1) would be the permutation of
, where * is the empty space. Of course one can see that this is the same as
(2 * 3 1) .
In a similar way, (2 * 1) would be the permutation of
 to
to
 .
As the 3 is not mentioned, there is an implication that it is left in its original
position. Thus the impossible arrangement seen previously would have a cycle
from the home state of the form (2 3) , which can easily been
seen to be an interchange that is not a legal permutation. It shall be seen later
how to tell generally if a particular permutation is legal for a particular
starting state.
.
As the 3 is not mentioned, there is an implication that it is left in its original
position. Thus the impossible arrangement seen previously would have a cycle
from the home state of the form (2 3) , which can easily been
seen to be an interchange that is not a legal permutation. It shall be seen later
how to tell generally if a particular permutation is legal for a particular
starting state.
Cycles can be strung together to get more permutations, which will be especially
useful for the 4 by 4 grid later on. If for example (2 * 1)
is performed to the home state then
(1 2 3 *) , as long as each individual
cycle is legal for the previous state, the combination of them will also be
possible. Permutations describe the interchanges between tiles and so combining
them will not necessarily produce permutations that can be performed by sliding
tiles in those orders; a cycle could represent an interchange that could be possible
by another, longer cycle of sliding permutations.
One can differentiate between types of cycles by breaking them up into
single cycles. For example (2 1 3 *) can be written
(2 1)(2 3)(2 *) which is applied by following each number
through the cycles. This called an odd permutation as it has an odd number of
products. In the same way (2 * 1)=(2 *)(2 1) is even.
Notice that the length of an odd permutation is an even number, and vice
versa. Combining two permutations of the same type is even, but combining an
odd and even permutation will be odd.
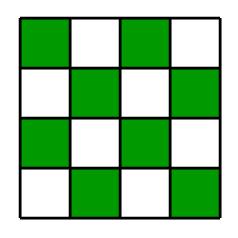 These same rules can be applied to the 4 by 4 grid, by permutations of squares
or rectangles of any size. One can tell that the solution will need to be an even
permutation if the empty space is left in its home slot. (See following pictures and
text.) Indeed it can be said that if the empty space is originally on any of the
green squares, the solution will be an even permutation, but if the space is on a
white square, an odd permutation is needed. These can be described by parity;
if there is a solution, one says the problem has even parity ie that the starting
state has the same parity as the home state. This is why only half the possible
arrangements are solvable; half the time the problem has even parity, and half,
odd parity.
These same rules can be applied to the 4 by 4 grid, by permutations of squares
or rectangles of any size. One can tell that the solution will need to be an even
permutation if the empty space is left in its home slot. (See following pictures and
text.) Indeed it can be said that if the empty space is originally on any of the
green squares, the solution will be an even permutation, but if the space is on a
white square, an odd permutation is needed. These can be described by parity;
if there is a solution, one says the problem has even parity ie that the starting
state has the same parity as the home state. This is why only half the possible
arrangements are solvable; half the time the problem has even parity, and half,
odd parity.
One can see that this is true by looking at the home state:



By sliding the 12 down one permutation is performed (12 *)
which is odd. To get back to the home state therefore the solution will be an
odd permutation as the empty space was left on a white square. Similarly if the
starting state is (12 * 11) from the home state, one can
tell that the solution is possible with an even permutation. In the same way one
can look at any shuffled starting position:
 Here the permutations are
Here the permutations are
(1 11 10 9 2 3 4 7 12 13 8 * 6 15)(5 14)
which is a combination of two odd permutations so is even. The empty square is found
on a green position so one can say that this problem is solvable.

The 14-15 Puzzle and other problems
Now Loyd's 14-15 puzzle shall be examined: this is the starting state which
looks like this:
Even though this appears to be so close to the final solution, one can tell from
the cycle that it is not solvable, because (14 15) is an
odd permutation and the space on a green position, ie odd parity.

Other starting states that can be looked at are the effect of rotating the
grid clockwise 90 degrees. The permutation is
(1 4 * 13)(2 8 15 9)(3 12 14 5)(6 7 11 10)
which is a combination of 4 odd permutations which is itself even. The empty
space is on a white position so this problem (including the problem of having the
tiles on their sides) is unsolvable.

If one takes the problem of having the empty space at the beginning rather
than at the end, the permutation cycle is
(1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 *)
which is an odd permutation with the space on a green position so it is an
unsolvable problem.
Finding Solutions-Simple
Of course after working out whether a particular problem is solvable, it would
then be useful to be able to find a solution. One logical process to follow is to
get the tiles in place in order, ie by getting the 1 into place, then the 2,3,4
etc.
 However one may quickly find that by placing the 3 in place, the 4 can not
fit without disturbing the 3 again. From the work before, it is known that a
permutation of (11 4) on the top right-hand 2 by 2
grid is not legal by sliding so instead permutations of a 2 by 3 grid are used.
However one may quickly find that by placing the 3 in place, the 4 can not
fit without disturbing the 3 again. From the work before, it is known that a
permutation of (11 4) on the top right-hand 2 by 2
grid is not legal by sliding so instead permutations of a 2 by 3 grid are used.





This is the same as a permutation of
(4 10 6 *)(6 3 11 *)(11 * 4)(3 6 11 10 * 4)=
(11 6 * 4).
In a similar way, the 7 and 8 can be placed in the correct positions. The bottom two lines
will have similar problems; the 9 and 13 need to be in the right order then
cycled round to their positions, and finally one is left with another 3 by 2
grid with the 10 and 14 to be placed first like the 3 and 4, then the
last three rotated to get home!
Of course it makes sense to think about the other
numbers and where they should eventually end up, and so move them in those
particular directions.
 For the general case if a tile, B needs to get into a upper right corner (either of
the grid, or previously positioned tiles) in the order A B at the top, the cycle of moves
from this position is thus:
For the general case if a tile, B needs to get into a upper right corner (either of
the grid, or previously positioned tiles) in the order A B at the top, the cycle of moves
from this position is thus:
(A C B D E *)(D B C E *)(B A E C*) in terms of the legal
slides.
These motions can then be used for any part of the problem in a corner,
just mirror the permutation to fit the corner.
Finding Solutions-Fastest
Obviously trying to solve the problem like this is not the fastest (ie the one
with the least number of moves) as one tends to move some tiles in the
wrong direction unnecessarily as the first ones are concentrated on individually.
As one can see in arranging the corner piece, it is sometimes
necessary to go backwards to be able to go forwards, but these motions ought to be
limited where possible

A computer could be used to evaluate all possible solutions and then
show the quickest one. It would look at all possible moves at each node- where
there is a branching off of possible solutions.
For example in the previous problem (shown again to the left), the starting
position has a node of different 4 paths or branches; the 4, 9, 11 or 14 could
be moved. If the 9 is chosen to be moved, the new node would have 3 branches,
but the 9 would be discounted as it leads back to the original position.
One way of getting the computer to perform the search is to make it
evaluate possibilities at each node, to pick one path and follow it until either
the home state is reached or a dead end. If a dead end is reached, the computer goes
back to the last node and takes a different path. However, one can not be sure that
this is the fastest, as it discards all other possibilities once it has found a
solution. Instead the computer could examine all nodes that are one permutation from
the starting position. If none of these are the solution they are expanded to
nodes 2 single permutations away from the starting state, etc until the home
state is found, so this will be the shortest. This however is very complicated
and certainly not something a human could do easily. There are many sites on
the internet that have programs to find the quickest solution (see sources) so
instead the problem of whether a person can solve the fifteen puzzle in the
shortest solution will be examined.

One thing a human can do is to work out an heuristic or best fit- an estimate
of the number of moves a tile would take to get from a particular position on the
grid to the home state.
The heuristic really wants to be either optimistic or correct as it will show the
minimum number of moves expected to get home. It is worked out by looking at the
position of each tile in the starting state and calculating the number of moves it
would take to get to its home place if the space were adjacent to it, in the
direction of home. In the example, the 1 would need 4 moves to get home (so the
heuristic is 4), the 13 would need 3, the 3, 1 move. It is known that the heuristic
calculated in this way is optimistic or accurate, because if the empty space were to
the left of its position now, the 13 could get to its home place in the
heuristic's estimated number of moves. However as it is not, the heuristic would be
larger as the tile can not be simply lifted up. The heuristic of a
particular problem is just the sum of all the individual heuristics.
It would seem sensible to work out the total heuristic for a particular problem
and then follow the path of best fit where the value of the heuristic decreases.
For the example taken, the heuristic at the start would be
4 + 1 + 1 +...+ 3 + 3 + 3 = 36 for the tiles in chronological
order.
To decrease the heuristic, the 9 or 14 could be moved, as they are the only two
moves that move the tile closer to its home position. Moving one tile in its
home direction decreases the value of the heuristic by one. A person can keep
track of the moves made and where the corresponding best fit nodes are. When a
dead end is reached, the person should go back to the last node and examine the
other branches, until a solution is found. However in practice this does not work
out. It was seen from the process of moving corner pieces into position that it
is necessary to move tiles in what seems the wrong direction in order to solve
the problem.
In conclusion, a human can combine both ways of solving the problem; through
simple logical solving and by trying to move the tiles in the direction of best
fit. In this way a solution will be found that will be reasonably short, and
probably shorter than any solution the person would have found by trial and error.
Obviously it does not take into account the time needed to work out the heuristic
at the start. Hopefully, understanding the principles used in the fifteen puzzle
would help a person understand the problem and to find the best way to go about
achieving a solution, whether they want a solution that is fast in time or number of
moves, or just to solve it for fun.
Sources:
W. W. Rouse Ball, Mathematical Recreations and Essays, Chapter XI Miscellaneous
problems, 10th ED. Macmillan and Co. 1937.
John Ewing and Czes Kosniowski, Puzzle It Out - Cubes, Groups and Puzzles,
Cambridge University Press 1982.
www.geocities.com/dariuscooper/puzzle/
www.geocities.com/jaapsch/puzzles/fifteen.htm
mitglied.lycos.de/jkoeller/15puzzle.htm
MATH 308 Euclidean Geometry Project, 2002
Hazel Grant


 These are 3 of the arrangements of the grid, with the first picture being the home
state; 9 other arrangements can be found by cycling
the 1 round to a new position and then rearranging the 2 and 3. Of course there
are 4! = 24 possible arrangements, but the other 12 can not be reached by
simple sliding moves. They would be found by performing an interchange;
ie where one tile is moved to the position of another tile or the space, which in
turn is moved somewhere else, possibly to the first tile's original position.
These are 3 of the arrangements of the grid, with the first picture being the home
state; 9 other arrangements can be found by cycling
the 1 round to a new position and then rearranging the 2 and 3. Of course there
are 4! = 24 possible arrangements, but the other 12 can not be reached by
simple sliding moves. They would be found by performing an interchange;
ie where one tile is moved to the position of another tile or the space, which in
turn is moved somewhere else, possibly to the first tile's original position.
 (ie swapping two of the tiles). One can see that the following arrangement is
not possible from the home state by following legal moves (ie sliding not
lifting):
(ie swapping two of the tiles). One can see that the following arrangement is
not possible from the home state by following legal moves (ie sliding not
lifting):
 The Fifteen Puzzle has been around for over a hundred years, and has been a
craze for almost every generation. The basic form is of a 4 by 4 grid usually
made with sliding tiles in a tray. There are 15 tiles numbered 1 to 15 and the
16th place is empty as shown. Before play begins the tiles are randomly
scrambled by sliding to any starting position. The object of the game is then
to unscramble the tiles (by sliding, not lifting them) to get them into
consecutive order, with the space in the bottom right again. (This will be
referred to as the home position.)
The Fifteen Puzzle has been around for over a hundred years, and has been a
craze for almost every generation. The basic form is of a 4 by 4 grid usually
made with sliding tiles in a tray. There are 15 tiles numbered 1 to 15 and the
16th place is empty as shown. Before play begins the tiles are randomly
scrambled by sliding to any starting position. The object of the game is then
to unscramble the tiles (by sliding, not lifting them) to get them into
consecutive order, with the space in the bottom right again. (This will be
referred to as the home position.)









 However one may quickly find that by placing the 3 in place, the 4 can not
fit without disturbing the 3 again. From the work before, it is known that a
permutation of (11 4) on the top right-hand 2 by 2
grid is not legal by sliding so instead permutations of a 2 by 3 grid are used.
However one may quickly find that by placing the 3 in place, the 4 can not
fit without disturbing the 3 again. From the work before, it is known that a
permutation of (11 4) on the top right-hand 2 by 2
grid is not legal by sliding so instead permutations of a 2 by 3 grid are used.







