Special Relativity
I am sure we all have heard of the famous phrase E=mc2 and its inventor, Albert Einstein. Special relativity is one of two theories Einstein developed that changed modern physics forever. In this small tutorial, we will go over the basics of what Einstein postulated in his theory of special relativity and some of their repercussions. To start off, we will give a brief history of the classical view on relativity.
Classical Relativity
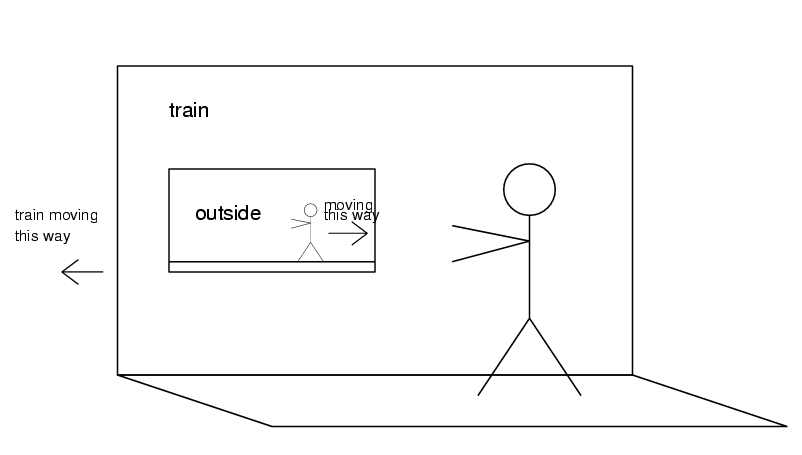
Just what is relativity? Well, have you ever stood inside a train and watched things outside go by as if they were moving and you were not? Just how do you tell if you are moving or if they are? The answer is, motion is relative. You can say either that you are moving and the outside is stationary or that you are stationary and the outside is moving. This is the basic idea of relativity. We call a certain way of looking at "who's moving and who's not", a frame of reference or just a frame (i.e.. a person outside is a frame of reference and you inside the train is another).
What if the person outside was moving in the opposite direction of the train? He will seem to have sped up relative to you, moving to the right. This is simple addition of velocity.
vperson' = vperson - vtrain
This formula says that the velocity of the person relative to you will be the velocity of the person relative to an inertial frame minus the velocity of the train relative to an inertial frame. So in this case, if the person is moving 1m/s and the train is moving -1m/s (negative meaning moving left) then the person will seem to be moving 2m/s relative to you. In the previous calculation, we take Earth as the inertial frame with the train and the outside person moving relative to Earth. The person will also say the same about you in the train. As another example, if we take the same scenario with the same speeds except that the person outside is NOT moving, then the person outside will seem to be moving 1m/s relative to you and the person outside will say that you are moving 1m/s relative to him.
Who's to say who's moving? The person outside can say you're moving and he's standing still or you can say
that you and the train are still and he's moving outside.
¡@
Now that we have a simple
understanding of relativity, let us go back in time to understand what
physicists had previously thought about the speed of light.
Let us say you are holding a flashlight and pointing it to the left of the
picture and you turn on the flash light and say that it travels at speed c. To
the person outside of the moving train, the speed of the light will be faster
because it is traveling on the train with you.
One of the experiments, named the Michelson-Morley
experiment, was conducted to test whether light had this property of
speeding up or down in different frames and whether it traveled like sound. As
we know, sound needs a medium to propagate. What
physicists thought was that an invisible material, called the
Ether, was what light used to propagate. The goal was
to show that interference
patterns existed, which would confirm that light had
both those properties. To the surprise of all physicists
around the world, there were no interference
patterns detected. Thus, there was proof that Ether did not exist and that
light did not change speeds in different frames of reference.
¡@
The animation shows that the light travels towards the mirror in the center. The center mirror will reflect part
of the light up and the rest goes right. When the light beams go into the detector, there was no interference
pattern because the light both arrive at the detector at the same time in phase.
¡@
¡@
Towards Modern Special Relativity
¡@
Let us examine the path that light takes from the center mirror to either the top or right mirror and back to the center mirror when the Earth is moving to the right. We don't have to consider the path from the light source to the center or from the center to the detector because both light beams will travel those paths. The only difference is the paths they take when they are split by the center mirror.
¡@
¡@
The animation shows the path that light takes as the apparatus and the light moves with the Earth
towards the right. Let's calculate the time (let's call it T1) it takes for the light to reach the mirror on the left.
¡@
given: v = velocity Earth is moving to the right
c = the speed of light
¡@
Time 1 = length between the two mirrors (L) / speed of light relative to Earth
= L / (speed of light - velocity of Earth) = L / (c - v)
¡@
Time 2 = L / (c + v)
Similarly to Time 1, but now light is moving the other way after reflecting off the right mirror
¡@
T1 = Time 1 + Time 2 = [L / (c - v)] + [L / (c + v)]
after some simplification...
T1 = 2L / c(1 - v2/c2)
¡@
The animation shows the path that light takes as the apparatus and the light moves with the Earth
towards the right. Let's calculate the time (let's call it T2) it takes for the light to reach the bottom mirror.
¡@
given: v = velocity Earth is moving to the right
c = the speed of light
¡@
length of triangular path (in red) = 2¡Ô L2 + (vT2/2)2 (from Pythagoras theorem z2 = x2 + y2)
T2 = length of path / speed of light = 2¡Ô L2 + (vT2/2)2 / c
after some simplification... and moving T2 to the left hand side...
T2 = 2L / c¡Ô 1 - v2/c2
¡@
As we had noted earlier, this experiment suggested that light did not change speed in whatever reference frame and that there was no interference pattern, thus if we took the difference between T1 and T2, we should get zero.
¡@
Time Difference = 0 = T1 - T2 = 2L / c(1 - v2/c2) - 2L / c¡Ô 1 - v2/c2
2L / c(1 - v2/c2) = 2L / c¡Ô 1 - v2/c2
2L / c¡Ô 1 - v2/c2¡Ô 1 - v2/c2 = 2L / c¡Ô 1 - v2/c2
¡@
The left hand side term has an extra 1/¡Ô 1 - v2/c2 term. This means that T1 needs an extra factor of ¡Ô 1 - v2/c2 multiplied to it to equal the right hand side. It turns out that moving things shrink in the direction of their motion. Thus, the L for the movement of light from left to right (with the Earth moving right), will shrink by a factor of ¡Ô 1 - v2/c2 , making the right hand side term equal to the left hand side term. This is known as the Lorentz-Fitzgeral length contraction.
¡@
This animation shows the length of a 4 inch ruler shrink as it moves faster and faster
¡@
¡@
Modern Special Relativity
¡@
In 1905, Albert Einstein wrote one of three great papers that changed the world of physics. One of which was on the topic of special relativity. In it, he postulated two things:
¡@
1. There is no observable difference between a frame at rest and a frame in uniform motion.
¡@
2. The speed of light is constant no matter what frame of reference you observe the light in.
¡@
Let us examine another repercussion of these postulates in addition to the length contraction mentioned earlier. If we look at the Michelson-Morley experiment again, we will find something very interesting. Let us look at the path that light takes between the top and center mirrors.
¡@
We found previously that T2 = 2L / c¡Ô 1 - v2/c2
Since the motion of the mirrors are to the right and the length, L, here is a measure of
vertical height, the L in this equation does not get shortened. Thus we can say this:
¡@
L = L'
¡@
We are saying that the length in an inertial frame (a frame where it measures the Earth's frame is moving at velocity v)
is the same as the length in it's own frame (Earth's frame).
¡@
Thus, T2 = 2L / c¡Ô 1 - v2/c2 = 2L' / c¡Ô 1 - v2/c2
¡@
In Earth's frame, where the apparatus is observed as not moving, the light just bounces up
and down without the sideways distance (vT2/2 terms).
¡@
Thus, 2L'/c = T2'
So, T2 = 2L / c¡Ô 1 - v2/c2 = 2L' / c¡Ô 1 - v2/c2
T2 = T2' / ¡Ô 1 - v2/c2
¡@
Here we see another important repercussion of the theory of special relativity, time slows down for a moving object. We see this by analyzing the above equation. If 'v/c' was 0.9, then square root of (1-0.9) = 0.316. Thus, T2 = T2' / 0.316, meaning that the time it took for light to traverse the up/down path between the mirrors, in a frame that measures the Earth's frame moving at uniform speed v, is 1/0.316 times the time measured for light to traverse the up/down path between the mirrors in the Earth's frame. This phenomenon, known as time dilation, occurs for things that do not move at the speed of light, although to a lesser extent.
¡@
This animation shows the moving clock's tics are much slower than the stationary clock's tics.
Terrel Rotation
¡@
One extraordinary repercussion of special relativity is the Terrel rotation effect. James Terrel reasoned that any object in motion will cause its image from the rear to be visible, depending on the angle of observation.
¡@
This animation shows a cube moving across the screen at the speed of light. Notice how the rear
(the edge labeled a on the cube) is seen by the observer and that the side of the cube (bottom
edge of the cube) appears stretched. (NOTE: we did not take into account length-contraction)
¡@
As the cube moves across, the "oldest" light from the top left corner will meet up with the "old" light from the bottom left corner and then meet up with the light from the bottom right corner to produce a distorted image of the cube. In the aforementioned, we say "oldest" light because the light from the top left corner was emitted before the other two corners. Then the bottom left corner meets up with this light, which is "old" compared to the light from the bottom right corner. Thus, we are looking at "historical" light from the cube when we get the full image of the cube as seen at the point "observer" in the picture.
¡@
Since the above cube is moving at the speed of light, then we will expect the width of the cube (top and bottom edges) to be shorter due to Lorentz-Fitzgeral length contraction. In fact the width will have to be zero (not shown in the above picture), as we can determine by looking at the formula. The height (left and right edges), however, will stay the same since it is not in the direction of motion. Therefore, we can conclude, from the picture above and our reasoning, that the cube will look as if its rear is coming at us!
¡@
¡@
References
¡@
- The Visual Appearance of Rapidly Moving Objects. Book from professor Bill Casselman.
¡@
- Modern Physics. Jeremy Bernstein, Paul M. Fishbane, Stephen Gasiorowicz. Prentice-Hall Inc., 2000
¡@
¡@
Created By Kevin Fung