The Schrodinger Equation is a postulate, and is regarded as an axiom of Quantum Chemistry. While no proof is possible, many of the postulates are “reasonable” based on their congruency to experimental results.
The time-independent Schrondinger Equation (for the one dimension case) utilizes the classical one-dimensional wave equation, deBroglie’s Equation, and energy relationships. The final equation is:
(h/4π)
● (d2Ψ/dx2) + U(x) ● Ψ(x) = E ● Ψ(x)
where:
h
is Planck’s Constant,
U(x) is the potential energy,
Ψ(x) is the wavefunction that describes the system,
and E is the overall energy of the system.
U(x) is the potential energy,
Ψ(x) is the wavefunction that describes the system,
and E is the overall energy of the system.
Particle in One-Dimension Box or Particle on a Line
For pedagogic purposes, the concept of the one-dimension box or singular line is often used to generate some of complex concepts of wave equations.
Assume there is a particle that exists between the region 0 and A. At both 0 and A, there is an infinite potential, which forces the particle to stay inside these bounds. The probability of find the particle outside of these bounds is zero.

The particle experiences zero potential within these bounds, so it may freely move around. When we apply this to the Schrodinger Equation, the second term drops out, so the net result is:
(h/4π)
● (d2Ψ/dx2) = E ● Ψ(x)
or
(d2Ψ/dx2) + (8π2mE/h2) ● Ψ(x) = 0
or
(d2Ψ/dx2) + (8π2mE/h2) ● Ψ(x) = 0
where:
h
is Planck’s Constant,
Ψ(x) is the wavefunction that describes the system,
E is the overall energy of the system,
and m is the mass of the particle
Ψ(x) is the wavefunction that describes the system,
E is the overall energy of the system,
and m is the mass of the particle
It can also be written in a more familiar way as:
(d2f/dx2)
+ (k) ● f(x) = 0
where
k
is a constant
Many mathematicians will recognize that the solution probably uses cosines and sine. Hence, Ψ(x) behaves in a harmonic or sinusoidal wave. The energy of the system is also quantized, since it can only take on certain, discrete values, which happen to be solutions of the system. The presence of the 8π2 forces the system to have a phase that has π in its denominator. The net result is a system which takes on integral values of cosines and sines. A general solution to this equation is:
Ψ(x)
= A cos kx + B sin kx
where:
A,B, are constants,
k = [(2mE)0.5]/h
h is Planck’s Constant,
and E is the overall energy of the system.
k = [(2mE)0.5]/h
h is Planck’s Constant,
and E is the overall energy of the system.
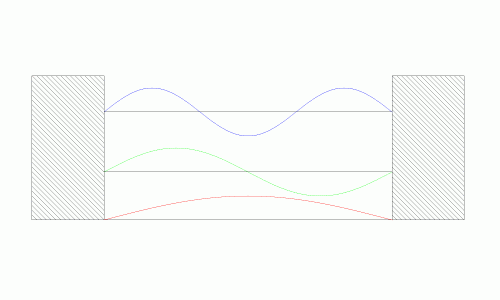
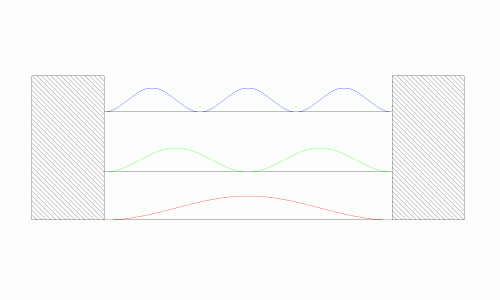
While this result may seem fairly abstract it provides two useful results. The first is that the energy of the system is quantized given the boundary conditions (the figure on the left). Since the particle can only travel in sinusoidal waves, there are only discrete energy levels it can take on. This should make some intuitive sense. If the standing wave was allowed to take any shape or form, it would eventually cancel itself out as it traveled from boundary point to boundary point. However, if it travels in a “controlled” sinusoidal path, then it will be able to neatly fit into the box without destroying itself. The energy of the system is the square of its position (the figure on the right). It shows that the system can only take on certain quantized values for total energy.
The second key result is that the function can be square normalized. The term square normalized simply means that the function, times its complement (including imaginary terms) must equal one when integrated over the entire region of interest. The region of interest is variable. In this particle in the box example, we integrate over the entire line from 0 to A. in the real world, we would integrate over all of x, y, and z.