In each case the picture shows a contour map, with each point in the set being plotted one of 128 colours. Here the colours go from red (= 1) via green (=0.5) to blue (=0). The first few pictures here are of harmonic functions which have Dirichlet boundary conditions 0 and 1 on the two sides of the square, and Neumann (i.e. reflecting) boundary conditions elsewhere. In physical terms, the picture can be interpreted as the temperature of a metal plate where the left and right edges are held at constant temperatures. (Red = hottest, and blue = coldest).
In this picture, the set is constructed in a similar fashion to the standard SC, except that each level each square is divided into a 5 by 5 block of smaller squares, and a cross shape (instead of a square) is removed.
This is similar to the previous picture, except a diagonal X is removed. As is clear from the picture, the boundary conditions at the point where two squares meet diagonally are that the process (or heat) can't cross between the squares.
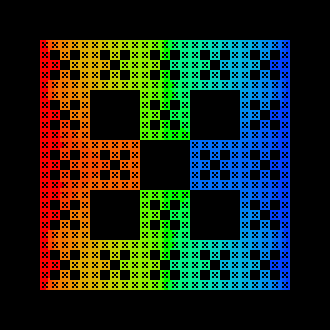
Click here to see the same GSC, but at level 4.
This picture shows a Sierpinski carpet in `harmonic coordinates'. If h_1(x) is the harmonic function in the pictures above, and h_2 is its rotation by 90 degrees, this is the image of the SC under the map which sends x to (h_1(x),h_2(x)).
Return to my home page